欧几里得考点三角函数讲解 这些公式和例题很重要

马上就要迎来了欧几里得考试了，本期想来给同学讲解的是欧几里得考点之一的三角函数，下面就来看看有哪些公式和值得看的例题！

SINE law

Cosine Law

a^2 = b^2 + c^2 − 2bc cos A

b^2 = a^2 + c^2 − 2ac cos B

c^2 = b^2 + a^2 − 2ab cos C

Area relations

The area of triangle ABC = |4ABC| = 1/2 ab sin C = 1/2 bc sin A = 1/2 ac sin B.

Area of an equilateral triangle

The area of an equilateral triangle of side length s is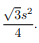

Heron’s formula

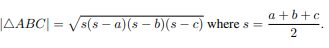
Trigonometric Identities

Related Angle Identities

sin(180◦ − θ) = sin θ cos(180◦ − θ) = − cos θ

Draw graphs of

y = A sin(kx + d) 

y = A cos(kx + d) 

y = tan x

例题

An airplane leaves an aircraft carrier and flies due south at 400 km/hr. The carrier proceeds at a heading of 60◦ west of north at 32 km/hr. If the plane has 5 hours of fuel, what is the maximum distance south the plane can travel so that the fuel remaining will allow a safe return to the carrier at 400 km/hr?

解析：

The first step in solving this problem is to draw a diagram (as shown). If we let x be the number of hours that the plane flies south then the distance that the plane flies south is 400x. The plane then flies a distance 400(5 − x). in the remaining time while the total distance the carrier flies is 5(32). Using these distances the cosine law states: (400(5 − x))2 = 1602 + (400x) 2 − 2 · 160 · 400x · cos 120◦ .

像欧几里得这类的国际竞赛不像学校里的考试那样，有很多固定的套路，会非常考验你的创造力和灵活的思维能力，如果感觉一个人摸索复习有点孤单，可以点击预约试听【橡沐欧几里得竞赛班课】——

点击

如何复习欧几里得竞赛呢？这个网站一定要知道

欧几里得竞赛能用计算器吗？可以使用但是有要求

查看。