牛津MAT考试学习资料 函数考点详解

最近我们不断接到关于包括牛津MAT考试在内的牛剑笔试的相关咨询。笔试本就是一场硬仗，在今年国际课程成绩普遍偏高的情况下，笔试考核更成为了学员展示学术能力和潜力的“第二战场。为此，橡沐教研团队将“笔试考点重点难点+复习方法详解”倾囊相授，今天我们就先从被牛津IC华威点名的MAT聊起吧，

（点击查看MAT考几分有望被录取）

2021牛津MAT考试时间倒计时已开启

今年MAT考试时间为11月3日（截止报名时间为10月15日），橡沐笔试教研团队将先从函数Functions开始，配合历年官方真题，依次拆解重点难点（下周起为大家带来递归和取值范围的考点解析）。
接下来，由夏导师做MAT函数考点做详解。

MAT Functions考点梳理

这次带来的是MAT中常见的关于Functions的考点。我们先从函数的定义着⼿，⼀个很恰当的⽐喻是"Functions are Machines"。怎么理解呢？

Functions are Machines

Informally, ⼀个函数 f: X→ Y是从集合X到集合Y 的⼀种规则，给每⼀个X⾥的元素x(输⼊/Input)分配了⼀个Y ⾥的元素f(x)(输出/output)，所以函数像极了⼀个机器。这⾥的X是函数的定义域(Domain)，Y是函数的值域(Range)，⽽且规则是⼀对⼀的。

换句话说，我们给这个机器任何⼀个输⼊，机器只会有⼀个输出；如果机器有太多选择(⼀对多)或者不知道选什么(没有定义)那么机器就会当机，换句话说，这就不是⼀个函数了。（学过Python的同学可以类⽐"def function(input): ... return output"是⼀个道理）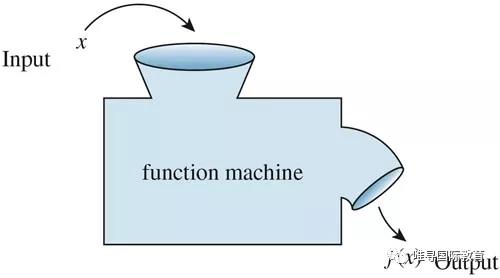

通过理解函数是⼀种规则，我们还可以把函数理解成“填空题”。⽐如说对函数 f(x) = x² ，这⾥表⽰的其实是⼀个规则，关于Input和Output的规则。In fact，它可以理解成：

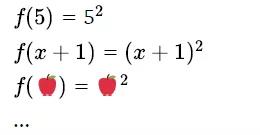
⼀个直观的例⼦就是MAT2011年的选择题G问：

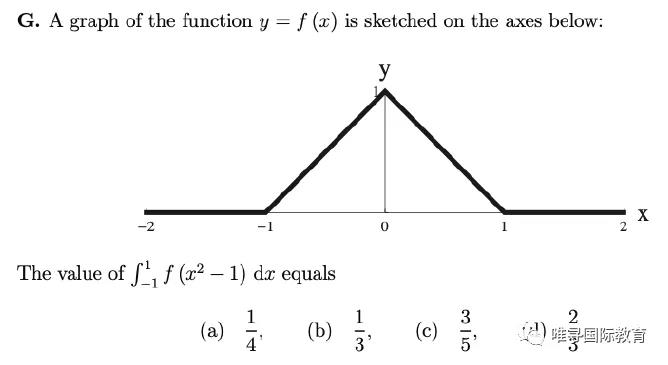
因为x²−1当x在-1和1之间的时候的取值范围必然是0和-1之间，然⽽如果在0到-1之间，函数图像告诉我们f( )=+1,所以Integral就被化简成了

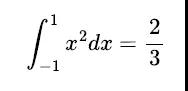
这样的理解也⽅便我们对导数⾥Chain Rule的理解：

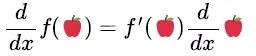
我们把函数的导数也理解成⼀种“填空题”。关于实函数⾥(Functions that are defined on Real numbers)，MAT有以下⼏个考点：

1.函数的奇偶性和对称Parity and Symmetry of a Function

2.函数图像的变化Transformations of a Function

3.函数的单调性Monotonicity of a Function

牛津MAT考试函数考点例题分析

篇幅所限，今天我们先从函数的奇偶性和对称性讲起，图像变化和单调性会在之后的文章中提及。

Parity and Symmetry of a Function

这块内容考核的⽐较灵活，因为对函数奇偶性的理解是⾼等数学阶段必要的素质，是重要的数学直觉。

我们先定义函数的奇偶性：

If f(−x)=f(x), then f(x) is said to be an even function.

If f(−x)=−f(x), then f(x)is said to be an odd function.

说⽩了就是把 −x丢给这机器，看看出来的值和f(x)的符号是否⼀样，如果⼀样的， 那就说明改变x的符号，函数值不变，所以函数是关于y轴对称的；如果符号相反，那就说明如果(x, y)在这个函数图像上，则(−x, −y)⼀定在这个函数图像上，这是⼀种中⼼对称。

In English, we say:

If f(x)is an even function, the graph is symmetric about the y-axis.

If f(x)is an odd function, the graph has rotational symmetry of order 2 about the origin. (这⾥的order 2指的是原图像旋转360度后和⾃⾝重叠了2次)

图片来自：网络

通过奇偶性我们可以培养⾃⼰判断函数对称性的直觉，⽐如sin(x) = sin(π−x)意味着(我们把x换成π/2 − x) sin(π/2 − x) = sin(π/2 + x)。

观察左右式，我们发现只有x 的符号变化了， 所以我们可以理解为函数f(x)=sin(π/2−x)是⼀个偶函数。

或者我们可以更形象的理解成，sin(x)函数从x = π/2出发，向左⾛和向右⾛相同的距离，函数值不变，这就是说函数关于x = π/2对称。
我们拿2013年牛津MAT考试Q3的(v)问举例：

标准答案的⽅法是根据(ii)的结果， 把A(k) 最general的表达式写出来后去⽐较coefficients，但是这不够⾼效。

我们从已知条件A(k) = A(2 − k)得知A(k)是关于k = 1对称的函数，换句话说，A(1 + k) = A(1 − k)，必然是偶函数。

同时，因为A(1+ k)是最⾼次不超过4的多项式，偶函数意味着这个多项式⾥不可以存在奇数项，所以我们的结论很直接：

如果我们把这种对称性的直觉利⽤好，有很多类似的题⽬可以有更⾼效的做法，又⽐如MAT2013Q2的最后⼀问：

题⽬希望我们从(*)出发，找出⼀个满⾜g(t) = (2t − 1)³的f(t)，这⾥标准答案的⽅法也是⽐较低效，通过展开整个g(t)，最后待定系数找到了⼀个。我们不妨带着函数的奇偶性的视⾓再去看看(*)式，f(t)−f(1−t)=g(t)=(2t−1) ³ (∗)
我们不难意识到t和1 − t表⽰的就是在t = 1/2左右对称的两个点，所以我们代⼊t=1/2 + x，更容易观察出对称性，得：
f(1/2+x)−f(1/2−x)=g(1/2+x)=(2x)³ =8x³ (∗)
此时，等式的右侧被简化成了8x³ ，正好是⼀个奇函数，这时候我们就可以做⼀个Educated Guess，如果f(1/2+x)是一个奇函数，那么f(1/2+x)−f(1/2−x)=2f(1/2+x)，这时我们不难发现f(1/2+x)=4x³ 就是⼀个满⾜条件的奇函数。所以我们的答案就可以⾮常简洁：f(x) = 4(x− 1/2)³就是⼀个满⾜条件的f(x)。

观察奇偶性也是⼀种“巧代”的思想，例如MAT2014J问，快节奏的⽅法确实是等式两   侧的同时积分，但是我们可以巧妙的代⼊−x，不难得到函数f(x)是偶函数，继⽽也很⽅便就解决了。

牛津MAT考试中函数的奇偶性和对称性知识点整理暂告一段落，离今年的MAT只剩1个月不到的准备时间了，如果你独自刷题找不到重点，欢迎点击预约试听【橡沐牛剑笔试班】——

从大量真题中找出

常见考点、题型、出题方式

将复习计划分出轻重缓解

更有教学团队+助教+顾问多人把关学习进度

与你一同面对牛剑申请前哨站

更多英国大学笔试攻略点击

2021新增的帝国理工学院专业笔试怎么准备？考纲分析与复习建议快收下

牛津MAT考试和PAT，通往梦校殿堂的2座高山