2022年STEP2真题解析来啦 今年的8道纯数题整体难度都挺高

本期我们想来给大家分享一些橡沐导师关于2022年STEP2真题解析，在今年的STEP2考试中，整体难度是高于去年的，可能也会导致分数线比之前的会低一点。

2022年STEP2真题

第一题的by parts有提示还是比较直接的，但是第二问的by parts 2次可能会不是那么明显，能够成功把图画出来的同学应该可以借助图像去解释本题的最后一问，作为2022年STEP2的开局，这题还是不错的。

解题过程：

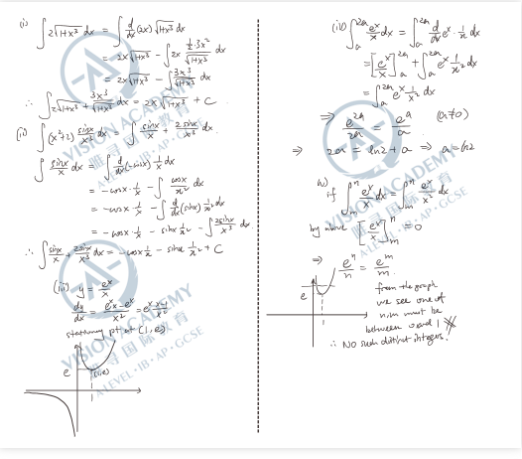
第二题的数列还是比较直接的一道题，关键是能够联想到等差数列的归形式；最后一部分如果可以结合第二部分的思路，会发现不需要一阶项，这可以简化解题过程。

Fibonacci数列是老朋友了，这道题的思路和09年step 2的第六题很类似，重点是与等比数列的比较而取得合理的缩放，题目中间段的描述可能让部分同学有点confused，导致最后一部分没有很好的完成。

第四题是非常popular的一道题，很多同学可以顺利的完成前几问，这些很有趣，它考验的是学生在观察过简单的函数之后，如何构造一些更复杂的函数，要记住，always make educated guess not wild guess，题目中还是有细微的hints的。

第五题是一道较为繁琐的不等式，关键是要意识到不等式取等号的情况可以发生在Boundary的上，后半段的恒等式其实就是证明柯西不等式的代数方法，只不过在题目的带领下，我们不需要应用柯西不等式，而是可以通过更为简单的argument得到最小和最大值。

第六题是一道微分方程的题，它考核的是学生是否可以根据题意构造出一个微分方程，然后再独立地解决它，这个的题目背景我们在上篇推文里也说过了，是orthogonal families；感兴趣的同学可以研究一下，这个topic在理论物理和应用数学中都很常见。

本张卷子唯一一道复数题是一道关于多项式和不等式的题，中间应用到了一个不等式的证明方法和13年step 3的第六题很像，利用多项式的系数的对称性和2019年step 2第三题以及2018年step 2的第一题类似，题目的后半段还是比较清晰的，背后的道理其实就是实数系数的多项式，永远可以被展开成linear and quadratic terms；这部分的证明在我们step的代数课里也时常提到，最后的韦达定理的应用也相对直接；不等式是难点。

这道matrices的题目是目前STEP2第一次涉及invariant line。2019年STEP3的第三题也考察了类似的内容，但主要涉及line of invariant points，内容比较基础，与高数的考察方式、难度都很接近，所以难度比我们今年这道题更低一些。这道matrices题目在invariant line的基础上，并且还巧妙结合了coordinate geometry、compound angle identities以及Vieta。整题计算量不大，主要注重思维的灵活性和知识点的联想综合能力。

以上就是2022年STEP2真题解析了，同学们感觉怎么样呢，STEP考试考得就是平时的训练与做题思维啊，如果您也想体验STEP考试，为自己的申请加油的话，赶紧点击这里了解更多牛剑笔试信息。

点击

STEP备考干货建议来了 要从题目类型入手

STEP考试如何科学备考呢？快来听听橡沐这2大策略

查看。